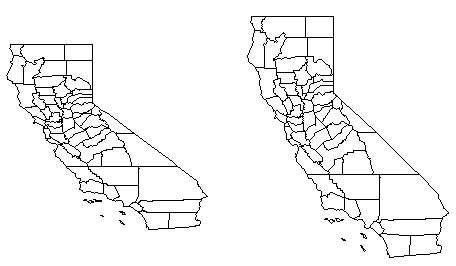
This shows the map of California before and after scaling. The map on the
right is scaled up in the Y dimension so the map does not appear compressed.
When you display maps based on latitude and longitude coordinates extending over a large region, they might appear somewhat distorted. This occurs because one degree of latitude is not equivalent to one degree of longitude. For example, consider a base map of the state of California (CA2000.GSB).

This shows the map of California before and after scaling. The map on the
right is scaled up in the Y dimension so the map does not appear compressed.
As an approximation, the distance covered by one degree of latitude at the equator is equal to the distance covered by one degree of latitude at the poles, and is approximately 69 miles. This distance between degrees of latitude remains nearly constant over the globe, although it does vary slightly because the earth is not a perfect sphere. However, the distance between a degree of longitude decreases from the equator to the poles. For any latitudinal position, you can determine the length, in miles, between degrees of longitude based on the formula:
Distance covered by 1° of longitude (in miles) = cosine (latitude) x 69.172.
This equation assumes a Clark 1866 reference ellipsoid.
This table illustrates the change as you move from the equator to the poles.
Latitude |
Distance Covered by One Degree of Longitude |
0° (equator) |
69.172 miles |
30° |
59.904 miles |
60° |
34.586 miles |
90° (poles) |
0 miles |
Substitutions for units other than miles:
For kilometers, you can substitute the number 111.321 for 69.172 in the formula above.
For meters, you can substitute the number 111,321 for 69.172 in the formula above.
For feet, you can substitute the number 365,228 for 69.172 in the formula above.
So, how can you put this information to use? Remember that you are plotting degrees of latitude and longitude, but what you really want to show on the map are the correct distances. You must scale the longitude values correctly for the correct distances to be represented on the map. The scaling factor to apply for maps is based on the cosine of the latitude for the area you are working on.
To determine the scaling factors:
Determine the latitude for the parallel through the center of the map, and obtain the cosine for this latitude value. The center parallel in CA2000.GSB is approximately 37.27 degrees. The cosine of 37.27 is 0.80.
Click on the Map in the Object Manager to select it. The map properties are displayed in the Property Manager.
Click the Scale tab to set the X direction for the map. You can set either the Length (page units) value or the Map units per in. (cm.) value. The X Scale Map units is 1.72 inches in this example.
Uncheck the Proportional XY scaling box.
Multiply the X Scale Map units value by the cosine of the latitude, and enter this number into the Y Scale Map units field. 1.72 (X Scale Map units) X 0.80 (cosine of latitude) = 1.38 (Y Scale Map units). Enter 1.38 into the Map units per in. box under Y Scale.
The map is automatically updated.
Example
Consider a map of the state of Montana. When you plot the map on a one to one scale, the map appears stretched in the east-west direction. To understand this problem, consider that for Montana the latitude ranges from 44.36° to 49°. The latitude for the center of the map is determined from this to be 46.68°. The cosine of 46.68° is 0.686. The distance covered by one degree of longitude at this latitude is only 0.686 times the distance covered by one degree of latitude. To reduce the distortion on this map, you must correct for this difference.
Let's say you are plotting the map at an X scale of 1" = 2 map units (longitude). For the map to be scaled appropriately, you would plot the Y scale at 1" = 1.372 map units (latitude, 2 x 0.686 = 1.372). This effectively stretches the map in the latitude (N-S) direction. Now the map distances are nearly the same in the longitude and latitude directions.
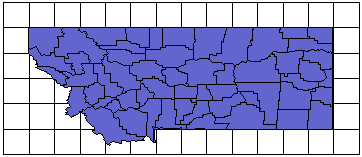
When the map is scaled so 1° of longitude equals 1° of latitude,
map distances are distorted. Notice that the graticules
form squares (equal spacing).
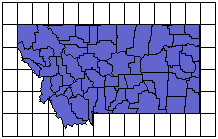
When
you apply scaling factors, map
distances are represented more
accurately. The rectangular spacing
of graticule lines indicate the
difference in scaling.
See Also